Függvények, relációk
Alapfogalmak
Ekkor A halmazbeli elemekhez B halmazbeli elemeket rendelünk: ezt nevezzük hozzárendelésnek vagy latin szóval relációnak.
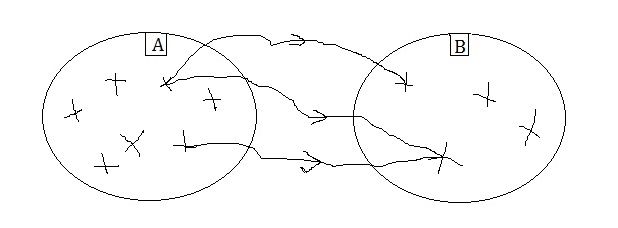
1. ábra: Hozzárendelés ábrázolása Venn-diagramon
Ezután térjünk rá magára a függvény fogalmára; ehhez először definiáljuk az egyértelmű hozzárendelés fogalmát.
Egy hozzárendelés/reláció egyértelmű, ha minden alaphalmazbeli elemhez legfeljebb egy képhalmazbeli elemet rendelünk.
Innen pedig már adódik a függvény definíciója:
Az egyértelmű hozzárendelést függvénynek nevezzük.
Ebből rögtön láthatjuk, hogy az 1. ábrán szereplő hozzárendelés nem függvény, hiszen van olyan alaphalmazbeli elem, melyhez 2 képhalmazbeli elemet is rendeltünk. Azt is észrevehetjük, hogy nem szükséges minden alaphalmazbeli elemhez bármit is rendelnünk, mint ahogy az sem szükséges, hogy minden képhalmazbeli elem hozzá legyen rendelve valamihez. Lényeg, hogy legyenek olyan alaphalmazbeli elemek, melyekhez rendelünk valamit a képhalmazból, és amennyiben függvényt szeretnénk, akkor ez a hozzárendelés legyen egyértelmű. Fontos hangsúlyozni, hogy az egyértelműség mindig a hozzárendelés irányában értendő: vagyis minden alaphalmazbeli elemhez csak 1 képhalmazbeli elemet rendelünk, ugyanakkor egy képhalmazbeli elem több alaphalmazbeli elemhez is hozzá lehet rendelve, ettől még a hozzárendelés függvény marad. Így például az alábbi hozzárendelés függvénynek tekinthető: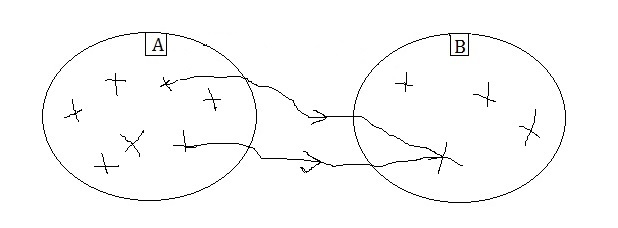
2. ábra: Egyértelmű hozzárendelés
De miért van a függvényeknek a relációkon belül is kitüntetett szerepe?
Kölcsönösen egyértelműek vagy más szóval egy-egy értelműek (injektívek) azok a függvények, amelyekben minden képhalmazbeli elem legfeljebb egy alaphalmazbeli elemhez lett hozzárendelve.
Itt az odafelé egyértelműséget már nem kell hangsúlyozni, hiszen a magában a függvény fogalmában benn van. Ezen kívül még néhány fontos definícióval adós vagyok, ezek közé tartozik az értelmezési tartomány, az értékkészlet, illetve a függő és független változó fogalma. Ezek azért fontosak, mert segítségükkel gördülékenyen tudunk beszélni a függvényekről, anélkül, hogy hosszas körülírásokba és magyarázkodásokba kellene bocsátkoznunk. Kezdjük is az értelmezési tartománnyal:Egy hozzárendelés értelmezési tartománya azon alaphalmazbeli elemek összessége, melyekhez rendeltünk valamilyen képhalmazbeli elemet.
A definíció alapján is látszik tehát, hogy korántsem feltétlenül az egész alaphalmaz jelenti az értelmezési tartományt: lehetnek olyan alaphalmazbeli elemek, melyekhez a függvény vagy reláció nem rendel semmit. Fontos hangsúlyozni, hogy értelmezési tartománya nem csak a függvényeknek, hanem minden relációnak van. Az értelmezési tartomány jelentőségét tanulmányozhatjuk akár az autós példán: nem feltétlenül tartozik minden autóhoz rendszám (pl. a használatból kivont, de le nem bontott autókról rendszerint leszerelik a rendszámot, ugyanis amíg rajta van a rendszám, adót kell utána fizetni). Az értelmezési tartománynak tehát ezek az autók nem részei, hiszen nem rendelt hozzájuk a függvény semmit; ugyanakkor az alaphalmaznak részei, mivel autók.Egy hozzárendelés értékkészlete azon képhalmazbeli elemek összessége, melyeket hozzárendeltük valamely alaphalmazbeli elemhez.
Az értékkészlet definíciója tehát az értelmezési tartományéval analóg, és láthatjuk, hogy az értékkészlet is messze nem feltétlenül a teljes képhalmazt jelenti: lehetnek pl. olyan rendszámok, amelyeket még semmilyen autóra nem szereltek fel, ezek a képhalmaznak részei, az értékkészletnek viszont nem.Ezután következzen az a két definíció, mellyel már régóta adós vagyok, vagyis a függvényszerű hozzárendelések két fő komponense: a független és a függő változó.
Független változónak nevezzük azon alaphalmazbeli elemeket, melyekhez a függvény hozzárendelt valamilyen képhalmazbeli elemet.
Függő változónak nevezzük azokat a képhalmazbeli elemeket, melyek hozzá lettek rendelve valamely alaphalmazbeli elemhez.
Az elnevezés szemléletes, hiszen valóban változnak, általában sokféle (akár végtelen sok) értéket vehetnek fel. A független változó azért független, mert bármit választhatunk az alaphalmazból független változónak, csak rajtunk múlik, hogy mit választunk, azaz nem függ semmitől. A függő változó viszont már nem lehet akármi: azt már a függvény hozzárendelési szabálya mondja meg, hogy egy adott, általunk választott független változóhoz milyen függő változó tartozik, tehát függ attól, hogy mit választottunk előzőleg független változónak. Összességében tehát elmondhatjuk, hogy a függvényszerű hozzárendelések két fő komponense a független és a függő változó; köztük pedig a hozzárendelési szabály teremt kapcsolatot.Jogosan merül fel a kérdés, hogy mindig a független változót válasszuk először ki? A válasz igen, hiszen a függvény egész egyszerűen így működik, ez a hozzárendelés iránya, azaz a függvény mindig a független változóhoz rendeli a függő változót, így előbb mindig ki kell választanunk egy elemet az alaphalmazból független változónak, majd ehhez a függvény hozzárendel egy és csakis egy függő változót a képhalmazból. Kivétel, ha olyan elemet választottunk az alaphalmazból, mely az értelmezési tartománynak nem eleme: utóbbi esetben a függvény nem rendel hozzá semmit, azaz nem jön létre hozzárendelés. Ugyanakkor arra is utaltam, hogy a hozzárendelés irányát megfordíthatjuk, ebben az esetben pedig a következő dolog történik: ami az eredeti függvényben a képhalmaz volt, az lesz az új függvény alaphalmaza, a régi függvény alaphalmaza pedig az új függvény képhalmaza. A hozzárendelési szabály pedig a következő lesz: minden elemhez rendeljük hozzá azt az elemet, melyhez az eredeti függvény őt hozzárendelte. Ezzel tulajdonképpen eljutottunk az inverz függvény fogalmához, a pontos definíció a következő:
Egy függvény inverze az a függvény, melyet úgy kapunk, hogy az eredeti függvény értékkészletének minden eleméhez hozzárendeljük azt az elemet, amelyhez őt az eredeti függvény hozzárendelte.
Azt is mondhatjuk tehát, hogy szerepcsere történt: az értékkészletből értelmezési tartomány lett az értelmezési tartományból pedig értékkészlet; illetve a független változó és a függő változó is helyet cserélt, ami az eredeti függvényben független változó volt, az az új függvényben függő változó lett és fordítva. Vegyük észre azonban, hogy az itt leírtak csak akkor működnek, ha az eredeti függvény értékkészletében levő minden elem csak egy alaphalmazbeli elemhez lett hozzárendelve; különben ugyanis a hozzárendelés megfordítása - vagyis hogy mindegyikhez hozzárendeljük azt, amihez hozzá lett rendelve - már nem lenne egyértelmű, vagyis nem kapnánk függvényt. Magát az inverz függvény elkészítését invertálásnak nevezzük, ekkor a fentiek alapján megfogalmazhatjuk az invertálhatóság feltételét:Egy függvény akkor és csakis akkor invertálható, ha kölcsönösen egyértelmű.
Nézzünk erre még egy konkrét példát. Köztudott, hogy különféle színű, fajtájú tehenek vannak, pl. tarka, fekete-fehér, szürke, stb. Ez alapján felállíthatunk egy olyan függvényt, hogy minden tehénhez rendeljük hozzá a színét. Ez valóban függvény, hiszen minden tehénnek csak egy színe van, nem lehet egyszerre tarka is, fekete-fehér is, szürke is, ez nyilvánvaló. Visszafelé viszont nem egyértelmű, hiszen ha azt tesszük fel kérdésként, hogy pl. melyik tehénhez tartozik a tarka szín, akkor nagyon sok jó megoldás lesz, hiszen, akár csak ha a vonatablakból kinéz az ember, láthatja, hogy nem csak egy tarka tehén van az országban. Tehát azt mondhatjuk, hogy a függvény nem kölcsönösen egyértelmű, és éppen emiatt nem is invertálható: az inverz függvény az lenne, hogy minden színhez rendeljük hozzá azt a tehenet amelyiknek ilyen színe van, de ez nem lenne egyértelmű, mert nagyon sok tehénnek van ugyanolyan színe. Viszont másképp is megközelíthetjük a problémát: rendeljük hozzá minden tehénhez a mintázatát. Azaz nem csupán azt, hogy milyen színe van, hanem azt, hogy pontosan hogyan állnak a foltok, mekkora méretűek stb. Ez viszont már kölcsönösen egyértelmű, mivel pontosan ugyanolyan mintázata nincs két különböző tehénnek; így a függvény invertálható is, azaz mintázat alapján egyértelműen visszakereshető, hogy melyik tehénről van szó.A gyakorlati életben és az elméleti matematikában is különösen nagy jelentőségre tettek szert a szám-szám függvények. Ezek semmiben nem különböznek lényegileg az eddig felsorolt függvényektől, csak annyi a specialitásuk, hogy számokhoz rendelnek számokat, vagyis az alaphalmazban és a képhalmazban levő elemek is számok. Vegyük észre, hogy rögtön az első említett példa is ilyen volt, hiszen a parttól való távolság és a vízmélység is számszerűen megadható adat, és ezek között teremtett összefüggést a hozzárendelés. A szám-szám függvények annyiban különlegesek még, hogy a hozzárendelési szabály, amellett, hogy szöveggel, körülírással továbbra is megadható, felírható matematikai műveletek segítségével is. Nézzünk erre rögtön egy példát!
Az 𝑓(𝑥)=3 függvény körülírással úgy fejezhető ki, hogy minden számhoz a 3-at rendeljük. Mivel bármilyen valós számhoz hozzá tudjuk rendelni a 3-at, az értelmezési tartomány ebben az esetben a teljes alaphalmaz, azaz a valós számok halmaza lesz. Ezt úgy is felírhatjuk, hogy 𝑥∈ℝ. A képhalmaz szintén a valós számok halmaza, az értékkészlet viszont ebből egyedül a 3, mivel a valós számok közül csak a 3-at rendeltük hozzá mindenhez. Maga az 𝑓(𝑥) jelölés is elemzésre szorul. Az f betű a latin (és innen az angolba is átvett) „function” szóból ered, ami függvényt jelent, de mivel a magyar „függvény” szó szintén f betűvel kezdődik, így innen is megjegyezhető. Az f egy műveletet jelöl, ez a művelet pedig nem más, mint maga a hozzárendelés. A mögötte levő zárójel az argumentumot jelöli, vagyis azt jelenti, hogy a zárójelen belül található dolgokra vonatkozik a művelet, jelen esetben a hozzárendelés. Ha ide konkrét számot írunk, akkor azt tudjuk meg, hogy ehhez a konkrét számhoz mit rendel a függvény; a fenti függvényben pl. 𝑓(5) azt mondja meg, hogy az 5-höz mit rendel a függvény, ez jelen esetben 3, hiszen ez a függvény mindenhez 3-at rendel. Az x a matematikában ismeretlent jelöl, vagyis azt jelenti, hogy bármilyen számot írhatunk a helyére az alaphalmazból. Az 𝑓(𝑥)=3 jelölés tehát azt jelenti, hogy bármilyen számot is vegyünk az alaphalmazból, a függvény mindegyikhez a 3-at fogja rendelni. Érdemes invertálhatóság szempontjából is megvizsgálni a függvényt. Mivel minden valós számhoz ugyanazt az egy számot, a 3-at rendeli, így nyilvánvaló, hogy nem lesz invertálható, hiszen ha a 3-hoz hozzá akarnánk rendelni minden olyan számot, amihez ő hozzá lett rendelve, akkor az összes valós számot hozzárendelhetnénk, vagyis visszafelé nem egyértelmű (emellett a többi számhoz meg nem tudnánk semmit rendelni, de ez ebből a szempontból nem lényeges).Vegyünk egy másik példát, legyen az 𝑓(𝑥)=2𝑥 függvény: eszerint minden valós számhoz hozzárendeljük a 2-szeresét. Ez nyilvánvalóan függvény, hiszen minden számnak egyértelműen csak egy bizonyos szám lehet a 2-szerese. Más részről kölcsönösen egyértelmű is, mivel biztos, hogy 2 különböző számnak a 2-szerese is különböző lesz; azaz minden képhalmazbeli elem csak 1 alaphalmazbeli elemhez lett hozzárendelve. Ha megfordítjuk a hozzárendelés irányát, akkor a következő függvényt kapjuk: rendeljük hozzá minden számhoz azt a számot, aminek ő a 2-szerese. Ilyen számot minden szám esetén találunk, méghozzá minden számnak a fele az a szám, aminek ő a 2-szerese. Tehát az inverz függvény az lesz, hogy minden számhoz rendeljük hozzá a felét, képlettel leírva 𝑓(𝑥)=𝑥/2 . Szakszóval azt is mondhatjuk, hogy az 𝑓(𝑥)=2𝑥 függvény szürjektív l eképezés, mivel minden képhalmazbeli elem hozzá lett rendelve valamihez, hiszen minden valós számhoz találunk olyan számot, amelynek ő a 2-szerese. Azt is láthattuk, hogy a függvény kölcsönösen egyértelmű, azaz idegen szóval élve injektív. Azokat a függvényeket, melyek egyszerre injektívek és szürjektívek, bijektívnek nevezzük. Az 𝑓(𝑥)=2𝑥 függvény tehát bijektív, ami röviden összefoglalva annyit jelent, hogy az összes alap- és képhalmazbeli elem összepárosítható a függvény által.
Következő példánk legyen az 𝑓(𝑥)=3𝑥+1 függvény, mely minden számhoz a 3-szorosánál 1-gyel nagyobb számot rendeli. Az előzőhöz hasonló meggondolásokkal itt is belátható , hogy a függvény kölcsönösen egyértelmű, sőt bijektív, inverze pedig az 𝑓(𝑥)=(𝑥−1)/3 függvény.Meglehetősen tanulságos az 𝑓(𝑥)=𝑥2 függvény, mely minden számhoz a négyzetét rendeli. A hozzárendelés egyértelmű, hiszen minden számnak csak egy négyzete van, tehát valóban függvénnyel van dolgunk. Nézzük, mi a helyzet a kölcsönös egyértelműséggel! Fordítsuk meg a hozzárendelést, vagyis rendeljük hozzá minden számhoz azt a számot, aminek ő a négyzete. Egyrészt rögtön láthatjuk, hogy az eredeti függvény nem szürjektív, hiszen a negatív számok semminek nem a négyzetei, mivel ha bármit négyzetre emelünk, az eredmény csak pozitív szám vagy 0 lehet; eszerint tehát a képhalmaz nem minden eleme része az értékkészletnek. Másrészt viszont azt is észrevehetjük, hogy pl. a 4 nem csak a 2-nek, hanem a -2-nek is négyzete, sőt az összes értékkészletbeli elemre igaz, hogy ha valaminek a négyzete, akkor annak az ellentettjének is négyzete, tehát visszafelé a hozzárendelés nem egyértelmű: a 0 kivételével az összes értékkészletbeli elem 2 alaphalmazbeli elemhez is hozzá lett rendelve. Összességében elmondhatjuk, hogy az 𝑓(𝑥)=𝑥2 függvény nem injektív, emiatt nem is invetrálható, emellett nem is szürjektív. Jogosan merül fel azonban a kérdés, hogy oké, nem invertálható a függvény, de mi van, ha mégis visszafelé szeretnénk gondolkodni, és arra vagyunk kíváncsiak, hogy egy konkrét szám minek a négyzete? Semmi gond, egyrészről, fel tudunk rá írni egyenletet, pl. ha arra vagyunk kíváncsiak, hogy a 9 minek a négyzete, akkor felírjuk, hogy 𝑥2=9, majd megoldjuk az egyenletet, akár szorzattá alakítással, akár úgy, hogy tudjuk: a 9 a 3 négyzete, de emellett a -3-é is, hiszen ha valami jó megoldás, akkor annak az ellentettje is jó megoldás, más jó megoldás pedig nincs. De az is lehet, hogy fontos nekünk, hogy a megfordítást függvényszerűen jelenítsük meg: erre is van megoldás! Egész egyszerűen szűkítsük le mesterségesen az értelmezési tartományt úgy, hogy a problémát okozó elemek legyenek kizárva. Mi okozza ebben az esetben a problémát? Az, hogy ha egy szám valaminek a négyzete, akkor annak az ellentettjének is a négyzete. Semmi más dolgunk nincs tehát, mint hogy megakadályozzuk azt, hogy egyidejűleg jelen legyenek az értelmezési tartományban a számok és ellentettjeik. Ezt úgy tudjuk megtenni, hogy vagy a negatív, vagy a pozitív számokat egész egyszerűen KIZÁRJUK. Ezt megtehetjük, hiszen, amint már írtam, független változónak azt választunk az alaphalmazból, amit csak akarunk, vagyis ha bizonyos elemeket egyáltalán nem szeretnénk felhasználni, ehhez is jogunk van, ekkor ezekhez az elemekhez nem fog rendelni a függvény semmit, vagyis ezek nem lesznek részei az értelmezési tartománynak. Nézzük meg pl. azt az esetet, mikor a negatív számokat zártuk ki, azaz leszűkítettük az értelmezési tartományt a nemnegatív valós számok halmazára. Ekkor az 𝑓(𝑥)=𝑥2 függvény kölcsönösen egyértelmű, így invertálható is, hiszen minden értékkészletben szereplő szám csak 1 alaphalmazbeli elemhez lett hozzárendelve; igaz ugyan, hogy annak ellentettjének is ő a négyzete, de mivel az ki lett zárva az értelmezési tartományból, így mégse lett ahhoz is hozzárendelve. Pl. a 4 csak a 2-höz lett rendelve, mert igaz ugyan, hogy a -2-nek is 4 a négyzete, de a -2 ki lett zárva az értelmezési tartományból, vagyis a függvény őhozzá nem rendelt semmit. Ebben az esetben a függvény inverze az 𝑓(𝑥)=√𝑥 . Hasonló módon belátható, hogy ha a nempozitív valós számok halmazára korlátozzuk az értelmezési tartományt, akkor 𝑓(𝑥)=−√𝑥 lesz az inverz függvény.
Mindeddig olyan szám-szám függvényeket hoztunk fel példának, melyek elvileg minden valós számon értelmezhetőek, legfeljebb az 𝑓(𝑥)=𝑥2 függvény esetében a végén „mesterségesen” leszűkítettük az értelmezési tartományt, hogy tudjunk invertálni. Vannak azonban olyan szám-szám függvények is, melyek még eredetei formájukban, a maguk „természetes” mivoltában sem értelmezhetőek az összes valós számon. Jó példa erre az 𝑓(𝑥)=1/𝑥 függvény, mely minden valós számhoz a reciprokát rendeli. Már amelyiknek van ilyen. Mert ha az x helyére 0-t helyettesítünk, akkor azt kapjuk, hogy 𝑓(0)=1/0, ami viszont értelmetlen kifejezés, hiszen 0-val nem tudunk osztani. Bármilyen más valós számmal viszont tudunk, így hát azt mondhatjuk, hogy az értelmezési tartomány a 0 kivételével az összes valós szám. A függvény kölcsönösen egyértelmű, hiszen minden szám csak egy bizonyos számnak a reciproka. Ha invertálni szeretnénk, akkor minden számhoz hozzárendeljük azt a számot, amelynek ő a reciproka. Ez viszont minden számnak a reciproka lesz, hiszen egy szám annak a számnak a reciproka, ami neki is a reciproka (más szóval azt mondhatjuk, hogy a reciprok viszony kölcsönös: két szám egymásnak lehet a reciproka). Vagyis az 𝑓(𝑥)=1/𝑥 függvény inverze önmaga. Emellett megállapíthatjuk még, hogy a függvény nem szürjektív: ugyanis a képhalmazból a 0 elem nem lett semmihez hozzárendelve, mivel a 0 semminek nem a reciproka. Megjegyzendő, hogy az 𝑓(𝑥)=𝑥 függvény inverze is önmaga, ezt hasonló módon beláthatjuk.Végezetül elérkeztünk oda, ami bizonyára már sokak vágya, akik a cikk olvasása során idáig eljutottak: mégpedig, hogy ábrázolni fogjuk a függvényeket koordináta rendszerben. De hogyan is tudjuk ezt megvalósítani? Ehhez egy analógiát használunk ki: nevezetesen azt, amit már az eddigiek során is láthattunk, hogy a függvényszerű hozzárendelés 2 komponensű: áll egy független és egy függő változóból. A sík pontjai pedig ugyanígy, ha felveszünk egy koordináta rendszert, 2 komponensből állnak: egy x és egy y koordinátából. Innen adódik a megoldás: a hozzárendeléseket ábrázoljuk síkbeli pontokként, mely pontok x koordinátája a független, y koordinátája pedig a függő változó értékével egyezzen meg! Pl. az 𝑓(𝑥)=1𝑥 függvény a 3-hoz az 13-ot rendeli, így ennek a hozzárendelésnek a koordináta rendszerben a (3;1/3) pont felel meg. A többi hozzárendelést hasonlóképpen ábrázolva a hozzárendelési pontok által kirajzolt vonalat nevezzük függvénygörbének. A függvénygörbék alakja rendkívül változatos lehet. Felrajzolásuk ugyanazon elv alapján történik: kiszámoljuk minél több hozzárendelési pont x és y koordinátáját (ehhez használhatunk táblázatot, melynek oszlopaiban egymás alatt találhatóak az összetartozó függő és független változók értékei, melyek a leendő hozzárendelési pont x és y koordinátái lesznek), majd a kapott pontokat berajzoljuk a koordináta rendszerben a megfelelő helyre. Ha pedig már elég pontunk van ahhoz, hogy lássuk a görbe alakját, akkor megfelelő alakú, jól illeszkedő vonallal összekötjük őket. De vigyázat! Nem feltétlenül jogos összekötni vonallal a pontokat, erről, ha precízen gondolkodunk előbb meg kell győződni, pont erről szól a függvény folytonossága, melyet minden egyes függvény esetében bizonyítani kell. Mindazonáltal általános sőt középiskolában sem szoktak ezzel bíbelődni, hanem egész egyszerűen összekötik a pontokat, ami az általunk jól ismert első és másodfokú, exponenciális illetve szögfüggvények esetében valóban helyes gyakorlat, csak előbb meg kellene bizonyosodni róla, hogy ez tényleg jogos. Utóbbi azt jelenti, hogy bizonyítjuk a függvény folytonosságát. Emellett a görbe menete szempontjából fontos tulajdonság a monotonitás, mindezekről a legközelebbi cikkemben lesz szó.
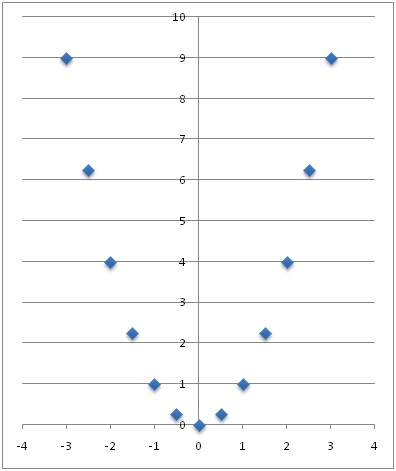
Az eddigiek során megismerkedtünk a függvényekkel és relációkkal. Megtudtuk, hogy a reláció / hozzárendelés azt jelenti, hogy két halmaz elemei között kapcsolatot teremtünk, az egyik halmaz elemeihez hozzárendeljük a másik halmaz elemeit. Amennyiben ez a hozzárendelés egyértelmű, akkor beszélhetünk függvényről. Megismerkedtünk az alapvető függvénytani fogalmakkal, mint független és függő változó, értelmezési tartomány, értékkészlet, illetve tanulmányoztuk a kölcsönös egyértelműséget és az invertálhatóságot szám-szám illetve egyéb gyakorlati, nem számokkal kapcsolatos függvényeken is. Végül áttekintettük, hogy hogyan tudjuk a függvényeket vizuálisan megjeleníteni koordináta rendszer segítségével. Példaként ábrázoljuk az 𝑓(𝑥)=𝑥2 függvényt:
Cikk letöltése